COVID-19 Discrete SEIR Model

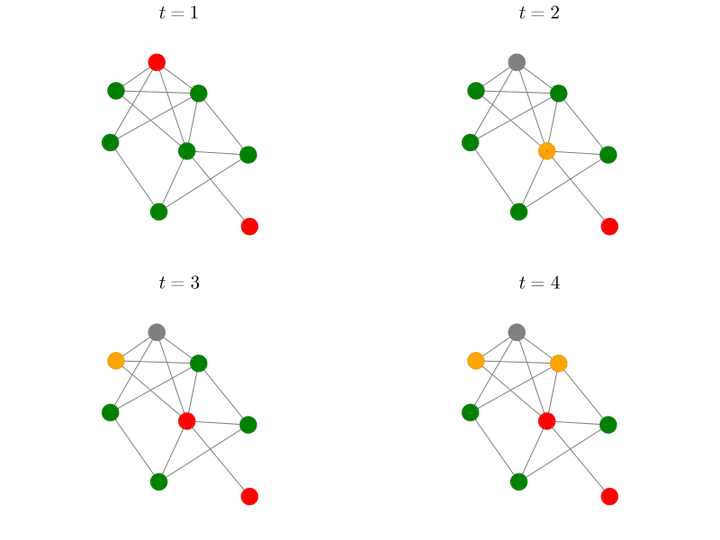
Figure: Visualization of the spread of an infection on a social network. Green vertices are susceptible, orange are exposed, red are infected, and grey are recovered.

Our team was given access to data on the course schedule and housing of the student population, which we used to build a network showing our predictions about physical contact between students. Our agent-based model was a discrete stochastic process based on the typical SEIR model that used the network data for a more accurate representation of the spread of the infection.

The model was executed as follows: first, students were assigned an initial state at random based on assumptions about how many students would attend the fall 2020 semester as either infected or exposed parties. For each iteration, students would change their state based on

• their current state
• the states of student that they had contact with
• several parameters representing the probability of contact and infection.

My role was to provide theoretical advice on predicting and preventing the spread of the infection using my knowledge of Markov chain processes and electrical network theory. I explained to the team that aside from highly-connected individuals (later termed super-spreaders), we needed to identify individuals that bridged usually separate populations (for example, athletes and musicians) and prevent them from having contact with more than one group.